Australia Telescope Compact Array

Frequency calculator

The following calculator determines the sky frequency of an ATCA observation (or some other observatories) for a particular source at a particular spectral line. Doppler correction, accounting for both dirurnal and annual motion is included in the calculation.

Source position:	(equatorial coordinates or source name)
Source systemic velocity:	km/s or redshift	Frame: LSR Barycentric
		Convention: Radio Optical z
UT Time (observing epoch):
Line:	or Rest frequency: MHz
Telescope:

Format of input parameters

The RA and DEC portions of the coordinate should be separated by a comma. Coordinates can by in the form hh:mm:ss,dd:mm:ss or in decimal hours and degrees (the coordinates are nominally in the J2000 frame). The calculator attempts to recognise other forms as well. Alternatively the name of a source can be given (the NED name resolver is used to convert this to a position).
The observing epoch gives the time of the observation. This is needed to compute the Doppler correction needed to account for the observatory's motion relative to the rest frame. The observing epoch can be given in any of the forms:
```
  yymmmdd
  yymmmdd:hh:mm:ss.s
  ccyy-mm-ddThh:mm:ss.s
  yymmmdd.dd
  dd/mm/yy
  dd-mmm-ccyy
```
where dd, mm and yy give 2-digit day-of-month, month and year respectively, mmm gives 3-character month (e.g. feb for February), and ccyy gives the 4-digit year (eg 2004). For example 04nov22 is 00:00 UT on 22 November 2004.

General note on velocities

Because the ATCA does not Doppler track, and because it does not correct for the systemic velocity of a source, the observer has to enter the actual sky frequency of the spectral line of interest. In converting to sky frequency, the observing frequency has to consider

The known systemic velocity of the source. There are two conventions in use for defining the velocity used - the so-called radio and optical conventions. There are also two commonly used rest frames - the solary system barycentre, and the so-called local standard of rest (LSR).
The additional velocity of the observatory relative to the rest frame.

Because of the Earth's motion, the frequency that corresponds to a particular velocity of an astronomical source will change with time. When observing spectral lines, many observatories continuously change the observing frequency to account for the effect of the Earth motion, and thus make a particular source velocity correspond to a single channel.

Note, however, that the ATCA does not Doppler track. Account of the Doppler correction is done in the off-line software.

Velocity conventions

The relativistic expression relating frequency to radial velocity is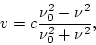

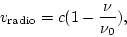
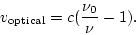
where v is the radial velocity, υ the observed frequency, υ₀ the rest frequency, and c is the speed of light. For various reasons, astronomers usually approximate this formula. There are two common approximations - the ``radio definition'',

and the ``optical definition'',

The radio definition has the advantage that points sampled at equal increments in frequency translate to equal increments in velocity. However the radio definition is now deprecated by the IAU, but this does not stop it being commonly used.

For high redshift objects, it is common to give the redshift of the object

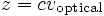
Rest frames

In defining a velocity, a rest frame must also be given. Because of the Earth's diurnal and annual motion (spin on its axis, and rotation around the Sun), the Earth's surface is not a good rest frame. The diurnal and annual motion have maximum velocity components of approximately 0.5 km/s and 30 km/s respectively. Two commonly used rest frames are the solar system barycentre (the dynamical centre of the solar system) and the local standard of rest (LSR) (which accounts for motion of the solar system relative to a collection of local stars). The LSR is generally used as the rest frame for Galactic astronomy, whereas the barycentric frame (often misnamed heliocentric frame - which is slightly different) is generally used for extragalactic work. An extra complexity is that there are a number of definitions of the LSR. The definition used is that the solar system barycentre is moving at 20 km/s in the direction of (RA,DEC) = 18 hours,+30 degrees (B1900) (this is called ``kinematic'' definition of the LSR).

Original: Bob Sault (22-Nov-2004)
Modified: Bob Sault (26-Nov-2004)